Los antiguos griegos pensaban que los seres vivos y los objetos estaban hechos de cinco elementos: tierra, fuego, aire, agua y el éter.
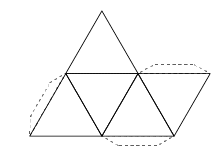
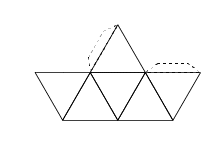
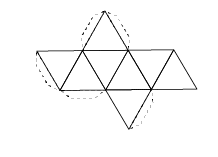
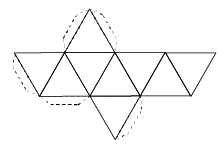
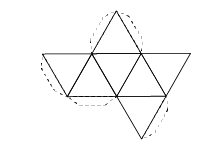
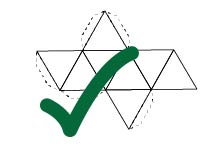
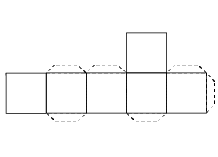
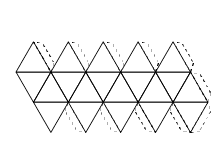
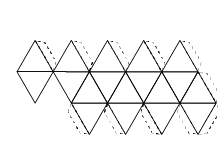
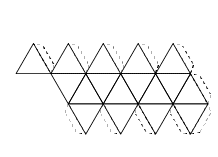
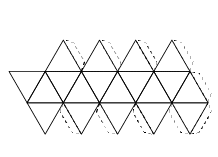
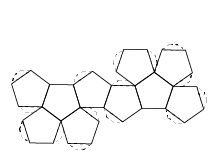
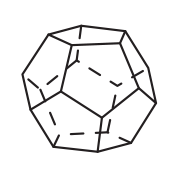
Estos cinco elementos estaban representados con los cinco poliedros regulares. Cada uno está formado por caras, que son las figuras geométricas que las componen, las aristas que son los lados de dichas figuras, y los vértices que son los puntos que unen dos o más aristas.
Platón tenía razón, así como los cinco elementos, los cinco sólidos platónicos son la esencia de la geometría, por lo tanto de la arquitectura, el arte; su belleza y perfección los hace únicos.